

Print("\nGiven x_test value is: ", x_test) P = np.polyfit(x, y, 2) # Last argument is degree of polynomial Using np.polyfit() method to implement linear regression The same is the case with a cubic polynomial of the form y=ax**3+bx**2+cx+d we need to have four constant-coefficient values for a, b, c, and d, which is calculated using the numpy.polyfit() function.
Similarly, in the case of a quadratic equation (having degree 2), which is of the form y=ax**2+bx+c, we need to have three constant-coefficient values for a, b, and c, which is calculated using the numpy.polyfit() function. If we want to fit these data points into a polynomial of various degrees like linear (having degree 1), which is of the form y=mx+c, we need to have two constant-coefficient values for m c, which is calculated using the numpy.polyfit() function. In the above program, we have created a dataset (x,y) using the np.arange() method, and the various points in the dataset are displayed. Print("\ncoefficient value in case of cubic polynomial:\n", z2)Ĭoefficient value in case of linear polynomial:Ĭoefficient value in case of quadratic polynomial:Ĭoefficient value in case of cubic polynomial: # calculating value of coefficient in case of cubic polynomial Print("\ncoefficient value in case of quadratic polynomial:\n", z1)
# calculating value of coefficient in case of quadratic polynomial Print("\ncoefficient value in case of linear polynomial:\n", z) # calculating value of coefficients in case of linear polynomial Print("Y values in the dataset are:\n", y) Print("X values in the dataset are:\n", x)
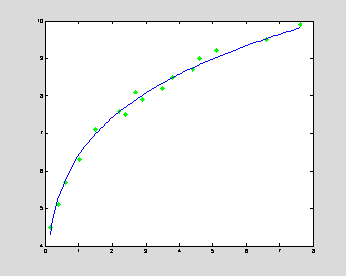
Programming Example: Program to show the working of numpy.polyfit() method. If Y is 2-Dimensional, the coefficients for the K th dataset are in p. This method returns an n-dimensional array of shape (deg+1) when the Y array has the shape of (M,) or in case the Y array has the shape of (M, K), then an n-dimensional array of shape (deg+1, K) is returned. It returns a ndarray, shape (deg+1,) or (deg+1, K) If cov=’ unscaled’, then the scaling is omitted as it is relevant because the weights are 1/sigma**2, with sigma being known to be a reliable estimate of the uncertainty. The covariance is by default scaled by chi**2/sqrt(N-dof), i.e., the weights are presumed to be unreliable except in a relative sense, and everything is scaled such that the reduced chi2 is unity. If provided and is not set to False, it returns not only the estimate but also its covariance matrix. For gaussian uncertainties, we should use 1/sigma (not 1/sigma**2). These are weights that are applied to the Y-coordinates of the sample points. When the value is set to false (the default), only the coefficients are returned when the value is set to true diagnostic info from the singular value decomposition is additionally returned. It acts as a switch and helps in determining the nature of return value. full: It’s an optional parameter of Boolean type Those singular values which are smaller than this relative to the largest singular value are going to be ignored. It describes the relative condition number of the fit. It should be an integer value and specify the degree to which polynomial should be made fit. Is a vector of length N+1 whose elements are the coefficients of Y = POLYVAL(P,X) returns the value of a polynomial P evaluated at Row vector of length N+1 containing the polynomial coefficients inĭescending powers, P(1)*X^N + P(2)*X^(N-1) +.+ P(N)*X + P(N+1)." "P = POLYFIT(X,Y,N) finds the coefficients of a polynomial P(X) ofĭegree N that fits the data Y best in a least-squares sense. This is MatLab's explanation of the function polyfit I need to do some calculations that involve curve fitting in javascript and can't for the life of me find an equivalent function. Essentially those functions in matlab do a curve fit based on two equally sized arrays depending on a specified polynomial. Desperately need a Javascript equivalent to polyval and polyfit functions that exist in Matlab.


 0 kommentar(er)
0 kommentar(er)
